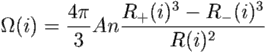
Tired Light Errors | Fads and Fallacies | Cosmology Tutorial: | Wright's Home Page
Stolmar's cosmological model uses a tired light redshift. The Earth is located in the center of a uniform density sphere of stars extending out to some maximum radius Rmax which is about 7 or 8 Hubble radii. The redshift factor 1+z is exponential with distance, and thus reaches a few thousand at the edge of the sphere. Starlight redshifted by this factor of a few thousand provides the cosmic background. However, this model does not agree with the observations and must be rejected:
In his CMB page on 27 July 2001 Stolmar gave the following equation for the solid angle covered by stars in a shell with radii between R- and R+,
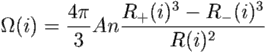
where A is the area of a star and n is the number density of stars. Stolmar gave this equation for the energy in the background radiation:
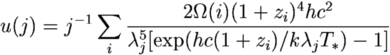
where the index j is the frequency in GHz. It is hard to determine exactly what is meant by this equation, since it appears to give the odd combination of energy density per unit wavelength divided by the frequency, but Stolmar also gave the equation for a blackbody:
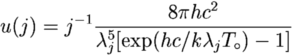
which can be used to normalize the previous equation. Now Stolmar also assumes (1+z) = exp(HR/c). If I take the limit of infinitesimally small shells in radius, I get a normalized integral for the specific intensity of the CBR which is
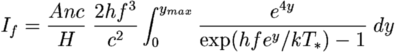
where y = H R/c, f is the frequency in Hz, and If is in [erg/cm2/sec/sr/Hz]. Stolmar prefers to use the doubling time of photon wavelengths, Hd, instead of the Hubble constant H, but these parameters are related by H = ln(2)/Hd. This formula has three free parameters: Anc/H determines the overall intensity scaling, T* determines the frequency scaling, and ymax determines the shape of the spectrum. Note that Anc/H is the optical depth per Hubble radius and it is very small in Stolmar's model [the total fraction of the sky covered by stars out to Rmax is roughly one part per trillion] so the use of the optically thin approximation here is appropriate. Also note that Stolmar assumes that all of the power emitted by the stars at redshift z reaches us, but with an apparent temperature redshifted to T*/(1+z). Normally in tired light models one allows for the loss of photon energy by a factor of (1+z) which would change the (1+z)4 = exp(4y) in the above equations to (1+z)3 = exp(3y). The only set of these parameters that agree with the FIRAS data on the CMB is ymax < 0.00005, T* = To = 2.725 K, and Anc/H = ymax-1. In this case the optical depth per Hubble radius is high so one has an opaque isothermal source: a blackbody. But real stars are not blackbodies, so even this limit will not actually work. When ymax is not infinitesimal, one gets a Rayleigh-Jeans low frequency tail rising to a peak corresponding approximately to a graybody with temperature exp(-ymax)T*, a Wien high frequency tail corresponding approximately to a graybody with temperature T*, and an If proportional to f -1 behavior between these two tails. The low frequency tail can approximate a blackbody for an appropriate choice of Anc/H. But this model can not simultaneously fit the data both above and below the peak unless ymax is infinitesimal. The examples given by Stolmar are extremely inconsistent with the FIRAS data on the CMB, as shown in Figure 1. Stolmar's comment about this discrepancy is "The higher calculated values on the right from the peak require closer examination of the reported processing of CMBR data". In other words, blame the data for not agreeing with his theory. However, these data have been confirmed by a separate experiment: see Gush, Halpern & Wishnow (1990, PRL, 65, 537).
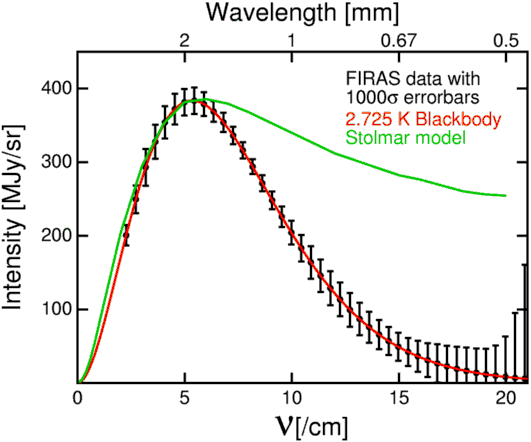
Figure 1: Stolmar's model with T* = 4000 and Rmax = 99 Glyr, which deviates from the FIRAS data by up to 13,000 standard deviations. This value of Rmax and Hd = 8.468 Glyr give ymax = 8.1 while my best match to Stolmar's curve is with ymax = 7.7. In this plot I use values read from Stolmar's graph. However, Stolmar recently changed Hd and has not updated these figures.
Since Stolmar's cosmology career on sci.astro started with the announcement of the DIRBE far IR background, it is interesting to plot his model on a much wider frequency range and compare not just to the CMB but also to the IR and optical backgrounds. This is shown in Figure 2. The long If proportional to f -1 section becomes a constant when one plots f If , and this behavior is quite contrary to the data, both the detections and the upper limits.
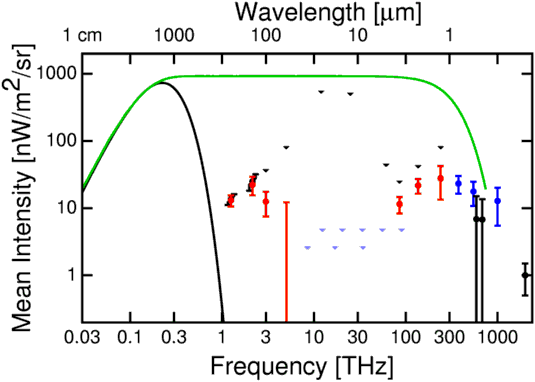
Figure 2: Stolmar's model compared to FIRAS, DIRBE, HST, groundbased and far UV measurements of the cosmic background. Since Stolmar's graphs do not extend to such short wavelengths, I have evaluated my integral version of his equations numerically. Green curve: Stolmar's model. Black curve, FIRAS BB fit. Black IR points: Hauser et al. (1998) on the CIRB. Red points: Wright et al. (2000, 2001) on the CIRB. Magenta upper limits from lack of TeV gamma-ray absorption. Blue points: Bernstein et al. (2001) on the optical background. Black optical and UV points: Toller; Dube et al.; and Hurwitz et al.
The stars at the edge of the sphere that produce the peak of the CMB are radiating at a time that is 7 or 8 Hubbles times ago. That is nearly 100 billion years, and only very low mass red dwarfs last that long. But low mass M dwarfs produce very little radiation, and Stolmar's model requires a lot of radiation. On 24 July 2001 Stolmar changed his H to 160 km/sec/Mpc, which alleviates this problem but disagrees with the data on the Hubble constant.
If we are not in the center of the Universe, a large dipole anisotropy is produced that has the spectrum of a graybody at temperature T*/exp(ymax). The observed dipole anisotropy has a different spectrum. Thus we must be nearly exactly in the center of the sphere of stars. A rough analysis of the FIRAS dipole anisotropy spectrum suggests that we must be centered within Stolmar's sphere of stars to within 1 part in 100,000 of Rmax, which means that the Milky Way could be the center, but the center of mass of the Local Group could not. Having the sphere of stars centered on the Local Supercluster is completely ruled out.
Tired Light Errors |
Fads and Fallacies |
Wright's Home Page
Cosmology Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 2001 Edward L. Wright. Last modified 29 Jul 2001