Ned Wright's Cosmology Tutorial

Part 1: Observations of Global Properties
Part 2: Homogeneity and Isotropy; Many Distances; Scale Factor
Part 3: Spatial Curvature; Flatness-Oldness; Horizon
Part 4: Inflation; Anisotropy and Inhomogeneity
Bibliography

Until a few hundred years ago, the Solar System and the Universe were equivalent in the minds of scientists, so the discovery that the Earth is not the center of the Solar System was an important step in the development of cosmology. Early in the 20th century Shapley established that the Solar System is far from the center of the Milky Way. So by the 1920's, the stage was set for the critical observational discoveries that led to the Big Bang model of the Universe.

Critical Observations

In 1929 Hubble [ 1, 2, 3] published a claim that the radial velocities of galaxies are proportional to their distance. The redshift of a galaxy is a measure of its radial velocity, and it can be measured using a spectrograph to determine the Doppler shift. The plot below shows Hubble's 1929 data:
Hubble's data

The slope of the fitted line is 464 km/sec/Mpc, and is now known as the Hubble constant, H_o. [Sometimes I will use "TeX" mode, so A_x means that x is a subscript, A_x, while A^x means that x is a superscript, A^x.] Since both kilometers and Megaparsecs (1 Mpc = 3.086E24 cm [the "E24" means multiply the 3.086 by 10 to the 24th power]) are units of distance, the simplified units of H_o are 1/time, and the conversion is given by

1/H_o = (978 Gyr)/(H_o in km/sec/Mpc)

Thus Hubble's value is equivalent to approximately 2 Gyr. Since this should be close to the age of the Universe, and we know (and it was known in 1929) that the age of the Earth is larger than 2 billion years, Hubble's value for H_o led to considerable skepticism about cosmological models, and motivated the Steady State model. However, later work found that Hubble had confused two different kinds of Cepheid variable stars used for calibrating distances, and also that what Hubble thought were bright stars in distant galaxies were actually H II regions. Correcting for these errors has led to a lowering of the value of the Hubble constant: there are now primarily two groups using Cepheids: the HST Distance Scale Key Project team (Freedman, Kennicutt, Mould etal) which gets 72+/-8 km/sec/Mpc, while the Sandage team, also using HST observations of Cepheids to calibrate Type Ia supernovae, gets 57+/-4 km/sec/Mpc. Other methods to determine the distance scale include the time delay in gravitational lenses and the Sunyaev-Zeldovich effect in distant clusters: both are independent of the Cepheid calibration and give values consistent with the average of the two HST groups: 65+/-8 km/sec/Mpc. These results are consistent with a combination of results from CMB anisotropy and the accelerating expansion of the Universe which give 71+/-3.5 km/sec/Mpc. With this value for H_o, the "age" 1/H_o is 14 Gyr while the actual age from the consistent model is 13.7+/-0.2 Gyr.

[Huchra's H_o history]

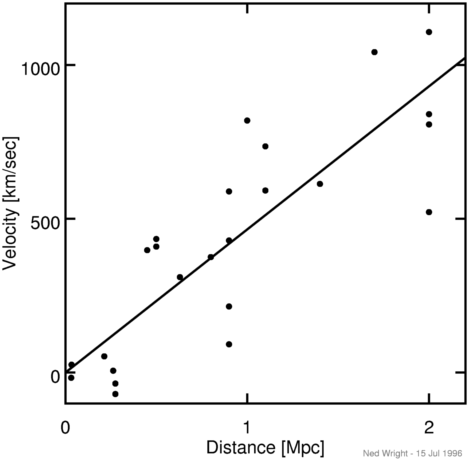
Hubble's data in 1929 is actually quite poor, since individual galaxies have peculiar velocities of several hundred km/sec, and Hubble's data only went out to 1200 km/sec. This has led some people to propose quadratic redshift-distance laws, but the data shown below on Type Ia SNe from Riess, Press and Kirshner (1996)

extend beyond 30,000 km/sec and provide a dramatic confirmation of the Hubble law,

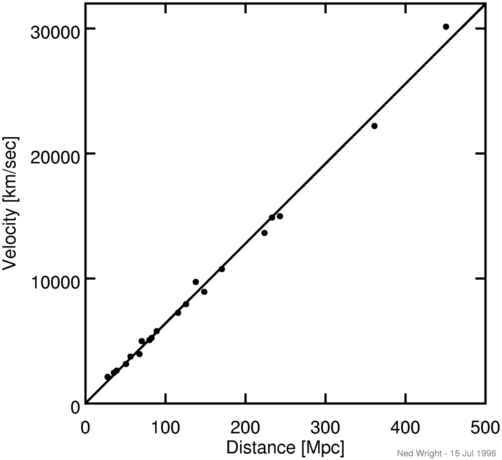
v = dD/dt = H*D

The fitted line in this graph has a slope of 64 km/sec/Mpc. Since we measure the radial velocity using the Doppler shift, it is often called the redshift. The redshift z is defined such that:

1 + z = lambda(observed)/lambda(emitted)

where lambda is the wavelength of a line or feature in the spectrum of an object. In special relativity we know that the redshift is given by

1 + z = sqrt((1+v/c)/(1-v/c))      so     v = cz + ...

but the higher order corrections (the "...") in cosmology depend on general relativity and the specific model of the Universe.

The subscript "o" in H_o (pronounced "aitch naught") indicates the current value of a time variable quantity. Since the 1/H_o is approximately the age of the Universe, the value of H depends on time. Another quantity with a naught is t_o, the age of the Universe.

The linear distance-redshift law found by Hubble is compatible with a Copernican view of the Universe: our position is not a special one. First note that the recession velocity is symmetric: if A sees B receding, then B sees that A is receding, as shown in this diagram:

which is based on a sketch by Bob Kirshner. Then consider the following space-time diagram showing several nearby galaxies moving away from us from our point of view (galaxy A, the blue worldline) on the top and from galaxy B's (the green worldline) point of view on the bottom.
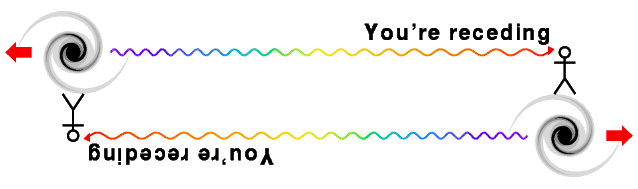
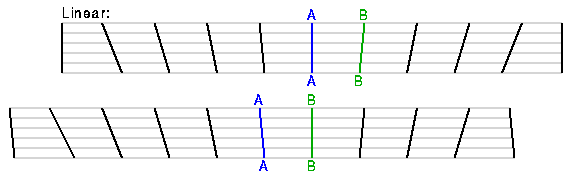
shift for linear law

The diagrams from the two different points of view are identical except for the names of the galaxies. The v(sq) = D² quadratic law, on the other hand, transforms into an anisotropic non-quadratic law when changing points of view, as shown below.
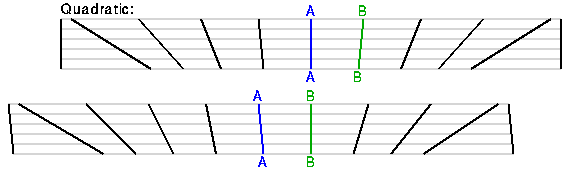
shift for square law

Thus if we saw a quadratic velocity vs. distance law, then an observer in a different galaxy would see a different law -- and one that would be different in different directions. Thus if we saw v(sq), then B would see much higher radial velocities in the "plus" direction than in the "minus" direction. This effect would allow one to locate the "center of Universe" by finding the one place where the redshift-distance law was the same in all directions. Since we actually see the same redshift-distance law in all directions, either the redshift-distance law is linear or else we are at the center which is anti-Copernican.

The Hubble law generates a homologous expansion which does not change the shapes of objects, while other possible velocity-distance relations lead to distortions during expansion.

The Hubble law defines a special frame of reference at any point in the Universe. An observer with a large motion with respect to the Hubble flow would measure blueshifts in front and large redshifts behind, instead of the same redshifts proportional to distance in all directions. Thus we can measure our motion relative to the Hubble flow, which is also our motion relative to the observable Universe. A comoving observer is at rest in this special frame of reference. Our Solar System is not quite comoving: we have a velocity of 370 km/sec relative to the observable Universe. The Local Group of galaxies, which includes the Milky Way, appears to be moving at 600 km/sec relative to the observable Universe.

Hubble also measured the number of galaxies in different directions and at different brightness in the sky. He found approximately the same number of faint galaxies in all directions, even though there is a large excess of bright galaxies in the Northern part of the sky. When a distribution is the same in all directions, it is isotropic. And when he looked for galaxies with fluxes brighter than F/4 he saw approximately 8 times more galaxies than he counted which were brighter than F. Since a flux 4 times smaller implies a doubled distance, and hence a detection volume that is 8 times larger, this indicated that the Universe is close to homogeneous (having uniform density) on large scales.

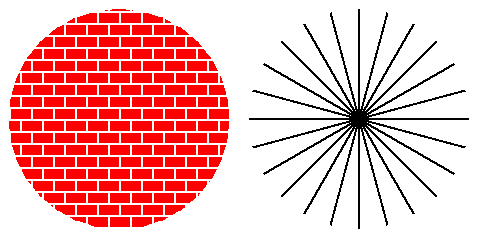
Homogeneous but not isotropic and vice-versa

The figure above shows a homogeneous but not isotropic pattern on the left and an isotropic but not homogeneous pattern on the right. If a figure is isotropic from more than 1 (2 if spherical) points, then it must also be homogeneous.

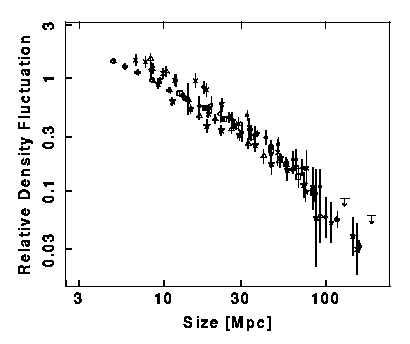
Of course the Universe is not really homogeneous and isotropic, because it contains dense regions like the Earth. But it can still be statistically homogeneous and isotropic, like this 24 kB simulated galaxy field, which is homogeneous and isotropic after smoothing out small scale details. Peacock and Dodds (1994, MNRAS, 267, 1020) have looked at the fractional density fluctuations in the nearby Universe as a function of the radius of a top-hat smoothing filter, and find:

delta(rho)/rho versus top-hat radius, H=65

Thus for 100 Mpc regions the Universe is smooth to within several percent. Redshift surveys of very large regions confirm this tendency toward smoothness on the largest scales, even though nearby galaxies show large inhomogeneities like the Virgo Cluster and the supergalactic plane.

The case for an isotropic and homogeneous Universe became much stronger after Penzias and Wilson announced the discovery of the Cosmic Microwave Background in 1965. They observed an excess flux at 7.35 cm wavelength equivalent to the radiation from a blackbody with a temperature of 3.5+/-1 degrees Kelvin. [The Kelvin temperature scale has degrees of the same size as the Celsius scale, but it is referenced at absolute zero, so the freezing point of water is 273.15 K.] A blackbody radiator is an object that absorbs any radiation that hits it, and has a constant temperature. 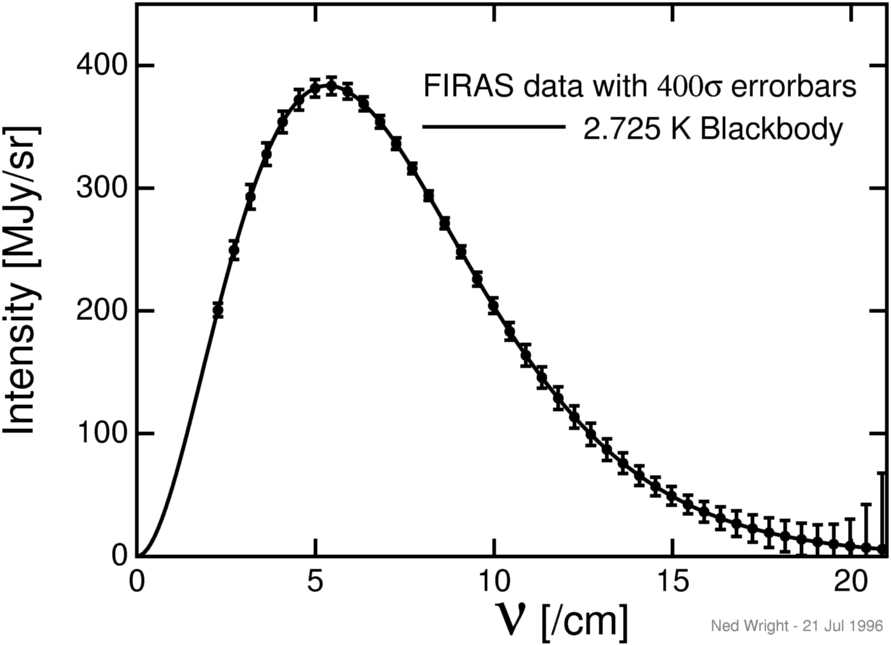Many groups have measured the intensity of the CMB at different wavelengths. Currently the best information on the spectrum of the CMB comes from the FIRAS instrument on the COBE satellite, and it is shown below:

The x axis variable is the wavenumber or 1/[wavelength in cm]. The y axis variable is the power per unit area per unit frequency per unit solid angle in MegaJanskies per steradian. 1 Jansky is 10^-26 Watts per square meter per Hertz. The error bars have been multiplied by 400 so they can be seen, but the data points are consistent with the radiation from a blackbody with T_o = 2.725 K.

The temperature of the CMB is almost the same all over the sky. The figure below shows a map of the temperature on a scale where 0 K is black and 3 K is white.

Thus the microwave sky is extremely isotropic. These observations are combined into the Cosmological Principle:

The Universe is Homogeneous and Isotropic

Another piece of evidence in favor of the Big Bang is the abundance of the light elements, like hydrogen, deuterium (heavy hydrogen), helium and lithium. As the Universe expands, the photons of the CMB lose energy due to the redshift and the CMB becomes cooler. That means that the CMB temperature was higher in the past. When the Universe was only a few minutes old, the temperature was high enough to make the light elements by nuclear fusion. The theory of Big Bang Nucleosynthesis predicts that about 1/4 of the mass of the Universe should be helium, which is very close to what is observed. The abundance of deuterium is inversely related to the density of nucleons in the Universe, and the observed value of the deuterium abundance suggests that there is one nucleon for every 4 cubic meters of space in the the Universe.

Next Section

Ned Wright's Home Page