
The chronometric cosmology proposed by Segal is incompatible with the cosmic microwave background (CMB). Segal predicts an angular size distance
D_A(z) = X/theta = R*sin(chi) = 2*R*sqrt(z)/(1+z),
where X is the physical size of an object, theta is the apparent angular size, [I will assume that theta << 1 radian and approximate sin and tan of theta] chi is an angle measuring distance around the spherical geometry of the chronometric cosmology, and R is the physical radius of the Universe in the chronometric model. The redshift is given by
z = tan^2(chi/2)
and the luminosity distance is given by
D_L(z) = sqrt[L(bol)/(4*pi*F(bol))] = sqrt(1+z)*D_A(z) = 2*R*sqrt(z/(1+z)).
Note that bolometric fluxes are integrated over all frequencies and have units of Watts/meter^2, and L(bol) is the total luminosity with units of Watts.
Now a blackbody (any opaque isothermal object) with temperature T and radius X has a luminosity L(bol) = 4*pi*X^2*sigma*T^4 where sigma is the Stefan-Boltzmann constant. The peak frequency of the spectrum is f(pk) = A*T/h, where A is close to 2.82 times Boltzmann's constant and h is Planck's constant. For a nearby source (z << 1), the relationship between the flux F(bol), angular radius theta, and temperature T is
F(bol) = L(bol)/(4*pi*D^2) = [4*pi*X^2*sigma*T^4]/(4*pi*D^2)
= theta^2*sigma*T^4 = theta^2*sigma*[h*f(pk)/A]^4
The observed quantities F(bol), f(pk) and theta have to satisfy this relationship for an object to appear to be a blackbody. Now consider a distant blackbody with redshift z. The peak frequency is shifted to
f(pk) = (A*T/h)/(1+z), and
F(bol) = L(bol)/(4*pi*D_L(z)^2) = [4*pi*X^2*sigma*T^4]/(4*pi*D_L(z)^2)
= theta^2 * [D_A(z)/D_L(z)]^2 * sigma * (1+z)^4 * [h*f(pk)/A]^4
In all respectable cosmological models, D_L(z) = (1+z)^2*D_A(z) so a redshifted blackbody looks like a blackbody. In Segal's chronometric cosmology, this is NOT true, D_L(z) = sqrt(1+z)*D_A(z), and
F(bol) = (1+z)^3 * theta^2*sigma*[h*f(pk)/A]^4
Thus by observing F(bol), f(pk) and theta for the cosmic microwave background one can determine the redshift at which the Universe becomes opaque. The FIRAS instrument on COBE adjusted the temperature of its calibrator (a local blackbody) so its f(pk) exactly matched the f(pk) of the CMB from the sky. It then removed the calibrator from the horn and looked at the sky to see if F(bol) changed. The change was a factor of 1.00001 +/- 0.00005 (Fixsen etal 1996, ApJ, 473, 576): in other words, NO change was seen, and an upper limit on the redshift at which the Universe is opaque is (1+z)^3 < 1.00001 + 3*0.00005, so z < 0.00005. Since quasars are observed at millimeter wavelengths (same as f(pk) for the CMB) out to z = 4.7, the chronometric cosmology FAILS the CMB test.
Note that Segal will always try to wiggle out of the CMB problem by stating that any theory that maximizes entropy while conserving energy will give a Planck function. But maximizing the entropy requires interactions to scatter photons giving isotropy and to absorb and re-emit photons, giving a Planck function once everything is isothermal. But these interactions don't occur in a vacuum - the "grain of sand" in the blackbody cavity is needed. We know the local region of the Universe (out to z = 4.7) is transparent and won't serve to create a blackbody. Since Segal's theory is static and homogeneous, there is no place and no time in the Universe that could have produced a blackbody. In Segal's book he assumes that the antipode (z = infinity) is the place where photon directions and energies are mixed up, but he forgets that everybody is somebody's antipode, so we should see this mixing locally. He also calculates a CMB energy density that is 100 times too large but doesn't care about this discrepancy. What I have shown above is that even if there were a place to make the blackbody, the CMB would still disagree with the COBE data unless that place were closer than z = 0.00005.
However, the chronometric model is not the only incorrect CMB theory from Segal. Let me quote from p. 117 of the proceedings of IAU Symposium 104, "Early Evolution of the Universe and its Present Structure", G. O. Abell and G. Chincarini eds., (c) 1983 (Dordrecht: Reidel), a discussion after papers presented by myself and Rowan-Robinson:
Segal - "The cosmic background radiation is, of course, not uniquely indicative of a Big Bang, but a Planck law for the background photons is implied by any temporally homogeneous theory in which the energy is modelled, as usual, by the infinitesimal time evolution generator. A very simply quasiphenomenological explanation of the Woody- Richard anomaly is a postulated non-vanishing isotropic angular momentum for the CBR in, for example, the vicinity of the Local Group. This provides a very good fit to their data, depends only on a single contemporary parameter rather than by hypothetical events at redshifts such as 200 or 1000, and automatically displaces the pure black-body law in the observed direction, rather than the opposite direction, as early discussion of perturbations of a Big Bang predicted. Therefore, isn't this scientifically more economical and in principle empirically accessible explanation of the Woody-Richards anomaly more natural than those presented that require a complete scenario hardly capable, in principle, of independent substantiation?"
Wright - "The Jakobsen, Kon and Segal model (1979, Physical Review Letters, 42, 1788, hereafter JKS) of the Woody and Richards (WR) spectrum has two basic flaws. The first flaw is that it does not fit the data if the low frequency results are included. The Planck brightness temperature of the JKS model is a nonincreasing function of the frequency, while the observed data rises from 2.7 K at low frequencies to 3.0 K at the peak, then falls to 2.8 K on the high frequency side of the peak. The JKS model matches the WR spectrum at the peak and higher frequencies, but predicts 3.4 K at low frequencies (see accompanying figure.)
The second flaw in the JKS model is that the predicted background is inhomogeneous and anisotropic (Wright, 1980, Physical Review D, 22, 2361). The local perturbation just proposed by Segal is also manifestly inhomogeneous. An inhomogeneous background violates the cosmological principle, and is thus incompatible with all modern cosmological models, including the chronometric cosmology of Segal."

This figure shows the JKS model fitting the Woody-Richards data (closed points) but missing the ground-based data (open points). The Woody-Richards distortion in the CMB was shown to be incorrect years before COBE was launched. The COBE spectrum is shown by the horizontal line, with the +/- 2 sigma uncertainty in the COBE data indicated by the width of the line. Click here for a GIF version of the figure or here for a Postscript version.
This story indicates a number of factors. One is that Segal always takes a very complicated approach. The other is that he is satisfied to fit a small part of the data, and then does not check to see that his model is consistent with all of the data.
When counting sources down to a flux limit S, one expects to see to a distance proportional to 1/sqrt(S), and hence to see a volume proportional to 1/S^1.5. Thus the number of sources brighter than a flux limit S, N(>S), should follow the law N(>S) = const/S^1.5 in Euclidean space. But the observed radio source and quasar counts are steeper than this law for medium to large S, giving an excess of moderately faint sources compared to the number of bright sources. In Segal's book, he notes that the flux per unit frequency for a source with luminosity per unit frequency L(nu) = C/nu^a is given by
F(nu) = [L(nu)*(1+z)^{2-a}]/[16*pi*R^2*z]
This flux reaches a minimum value for z = 1/(1-a) when a is less than 1 as it usually is for radio sources. There is an excess of sources at fluxes close to the minimum flux, and Segal used this mechanism to make a qualitative explanation for the radio source counts.
Wright (1987, ApJ, 313, 551) did the calculations to see whether a quantitative fit to the source counts was possible, and found that it was impossible to make a statistically acceptable fit to the source counts in the chronometric cosmology. Wright introduced a source count excess ratio
E(S1,S2) = (S1/S2)^{1.5} N(> S1)/N(> S2) for S1 < S2
and showed that E < 3*pi/2 in the chronometric cosmology, while the observed quasar counts had E > 17. Thus while Segal can produce a small excess of faint sources, he can not produce an excess that is as large as the observed excess.
In Segal's reply to this paper (1987, ApJ, 320, 135) he claimed that E could go to infinity in the chronometric cosmology in the limit S2 goes to zero. But since the flux S1 is positive, the limit S2 goes to zero violates the condition S1 < S2. It is sad to see that a math professor at MIT could have forgotten how to manipulate inequalities. I pointed out this error to Segal before his paper was published, but he went ahead and published his incorrect results.
The most unusual prediction made by Segal is that the redshift is a quadratic function of the distance, instead of the linear Hubble law. For z << 1 Segal then predicts that the flux should follow F = const/z, and since magnitudes are defined as m=Const-2.5*log(F), Segal predicts that m = 2.5*log(z) + M, where M is the absolute magnitude defined with a standard distance at z=1 instead of 10 pc. The Hubble law predicts that m = 5*log(z) + M. Soneira (1979, ApJL, 230, L63) made a test of this prediction using the average redshift of galaxies in magnitude bins, which I will denote as <z|m> for the mean redshift at a given magnitude. Soneira found m = 5*log(<z|m>) + CONST, so Hubble was right. Segal, however, likes to use the mean magnitude in a redshift bin, <m|z>, and finds that <m|z> = 2.5*log(z) + CONST. How can this be? It turns out that the mean magnitude in a redshift bin is strongly biased by the fact that galaxy samples are flux-limited. Galaxies are not all the same brightness, and in fact very faint dwarf galaxies are much more common than luminous galaxies like M31. In the observed samples, the very faint galaxies (large m) are missing, and thus <m|z> is biased downward. To study this bias one needs to know the relative number of faint versus luminous galaxies, known as the luminosity function. Schechter (1976, ApJ, 203, 297) found a luminosity function n(M) = const*10^{0.1*M}/exp(10^{0.4*(Ms-M)}) galaxies per unit volume per magnitude, using both field galaxies (assuming the Hubble law) and clusters of galaxies where no assumption about the redshift-magnitude law is needed. Other workers have found n(M) = const/exp(10^{0.4*(Ms-M)}) is a better fit. Approximate this as n(M) = const for M > Ms, and zero for M < Ms. Then the redshift-magnitude diagram will be populated with a density of galaxies proportional to z^2*dz for bright(z) < m < faint, where bright(z) = Ms + 5*log(z), and faint is the magnitude limit. In defining bright(z) I have assumed the Hubble law is correct. I can now easily find that <m|z> = (bright(z) + faint)/2 = 2.5*log(z) + (Ms+faint)/2. Thus Segal's analysis technique will bias the results to fit his theory. On the other hand Soneira's technique using <z|m> gives <z|m> = 0.75*10^{0.2*(m-Ms)}, so 5*log(<z|m>) = m + const. Segal has since introduced a new statistical technique that he calls ROBUST, but since the original claim of a quadratic redshift-distance law was due to a biased statistical technique, any method that agrees with the original biased analysis is also flawed.
I am fairly sure that the problem with ROBUST is caused by a gradual loss of completeness as the catalog limit is approached, but why should I bother to work this out? Segal is wrong on the CMB, wrong on the source counts, and wrong on the redshift-magnitude law. Three strikes and you're out is the popular criminal law these days, but in science it has always been ONE strike and you're out. That's why theorists invented free parameters, but the chronometric theory doesn't have any parameters except for the scale factor, so it makes very definite predictions which are WRONG.
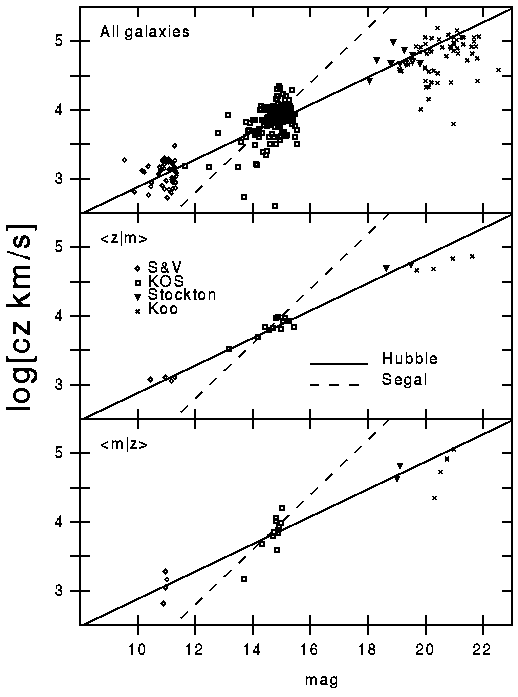
This figure shows the <m|z>, <z|m> and all of the magnitudes and redshifts for four samples of galaxies: Sandage and Visvanathan (1978, ApJ, 223, 707), Kirshner, Oemler and Schechter (1978, AJ, 83, 1549), the galaxies NOT associated with quasars in Stockton (1978, ApJ, 223, 747), and Koo (1982, in the proceedings of IAU Symposium 104). The three panels from top to bottom show all the galaxies, <z|m>, and <m|z>. Note that Segal's law definitely fits <m|z> for a SINGLE sample better than the Hubble law does, but different zero points are needed for each sample. This is expected because the different samples had different limiting magnitudes, and the bias in <m|z> depends on the flux limit. On the other hand, the Hubble law with a single zero point fits all the <z|m> points well, and even gives a better overall fit to <m|z> when all the samples are fitted simultaneously. Click here for the GIF version of the figure or here for Postscript version.
Noted netizen John Baez offers these memories of Irving Segal, his thesis advisor.
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 1996-2001 Edward L. Wright. Last modified 29-May-2001